Mi a korrelációs együttható?
A korrelációs együttható segítségével meghatározható, hogy mennyire erős a kapcsolat két változó között, és értéke -1,0 és 1,0 között lehet, ahol -1,0 negatív korrelációt és +1,0 pozitív kapcsolatot mutat. Figyelembe veszi a változók relatív mozgásait, majd meghatározza, hogy van-e kapcsolat közöttük.
Korrelációs együttható képlete
r = n (∑xy) - ∑x ∑y / √ (n * (∑x 2 - (∑x) 2 )) * (n * (∑y 2 - (∑y) 2 ))
Hol
- r = korrelációs együttható
- n = megfigyelések száma
- x = 1 st változó keretében
- y = 2 nd változó
Magyarázat
Ha van összefüggés, vagy mondjuk összefüggést két változó között, akkor jeleznie kell, hogy az egyik változó értéke megváltozik-e, akkor a másik változó is hajlamos az értékváltozásra, mondjuk konkrétan, amely lehet akár ugyanaz, akár az ellenkező irányba. Az egyenlet számláló része tesztet és az együtt mozgó változók relatív erősségét hajtja végre, az egyenlet nevező része pedig a számlálót skálázza úgy, hogy megszorozza a változók különbségét a négyzetes változóktól.
Példák
1. példa
Vegye figyelembe a következő két változót, x és y, és ki kell számolnia a korrelációs együtthatót.
Az alábbiakban a számításhoz adunk adatokat.

Megoldás:
A fenti egyenlet felhasználásával kiszámíthatjuk a következőket

Megvan a fenti táblázat összes értéke, n = 4.
Most adjuk meg az értékeket a korrelációs együttható kiszámításához.

Ezért a számítás a következő,

r = (4 * 25 032,24) - (262,55 * 317,31) / √ ((4 * 20 855,74) - (262,55) 2 ) * ((4 * 30 058,55) - (317,31) 2 )
r = 16 820,21 / 16 831,57
Az együttható a következő lesz:

Együttható = 0,99932640
2. példa
Az X ország növekvő gazdaságú ország, és független elemzést kíván készíteni a központi bankja kamatváltozásokkal kapcsolatos döntéseiről, függetlenül attól, hogy ezek befolyásolták-e az inflációt, és képes-e a központi bank ugyanezt ellenőrizni.
Az alábbiakban összefoglaljuk a kamatláb és az országban átlagosan uralkodó inflációs ráta összegzését.
Az alábbiakban a számításhoz adunk adatokat.

Az ország elnöke megkereste Önt, hogy elemzést végezzen és előadást tartson ezzel kapcsolatban a következő ülésen. Használjon korrelációt, és állapítsa meg, hogy a központi bank elérte-e célját vagy sem.
Megoldás:
A fent tárgyalt képlet segítségével kiszámíthatjuk a korrelációs együtthatót. A kamatlábat egy változónak, mondjuk x-nek, az inflációs rátát pedig egy másik változónak y-ként kezelni.

Megvan a fenti táblázat összes értéke, n = 6.
Most adjuk meg az értékeket a korrelációs együttható kiszámításához.


r = (6 * 170,91) - (46,35 * 22,24) / √ ((6 * 361,19) - (46,35) 2 ) * ((6 * 82,74) - (22,24) 2 )
r = -5,36 / 5,88
Az összefüggés a következő lesz:

Korreláció = -0,92
Elemzés: Úgy tűnik, hogy a kamatláb és az inflációs ráta közötti összefüggés negatív, ami a helyes összefüggésnek tűnik. A kamatláb emelkedésével az infláció csökken, ami azt jelenti, hogy általában ellentétes irányba mozognak egymástól, és a fenti eredményből kitűnik, hogy a jegybank sikeresen hajtotta végre a kamatpolitikával kapcsolatos döntést.
3. példa
Az ABC laboratórium magassággal és életkorral foglalkozik, és meg akarta tudni, hogy van-e valamilyen kapcsolat közöttük. Összegyűjtöttek egy 1000 fős mintát az egyes kategóriákhoz, és átlagos magasságot értek el abban a csoportban.
Az alábbiakban adunk adatokat a korrelációs együttható kiszámításához.

Számítania kell a korrelációs együtthatót, és arra a következtetésre kell jutnia, hogy ha van kapcsolat.
Megoldás:
Az életkorot egy változónak, mondjuk x-nek, a magasságot (cm-ben) pedig egy másik változónak y-ként kezelni.

Megvan a fenti táblázat összes értéke, n = 6.
Most adjuk meg az értékeket a korrelációs együttható kiszámításához.

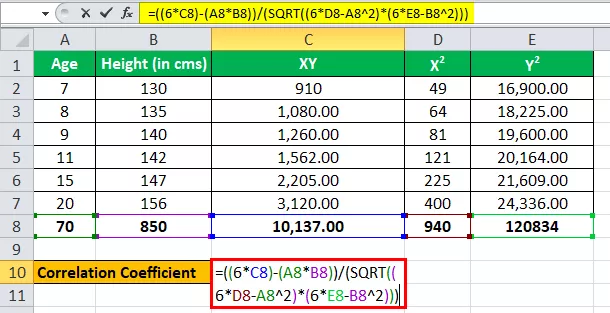
r = (6 * 10 137) - (70 * 850) / √ ((6 * 940 - (70) 2 ) * ((6 * 1,20 834) - (850) 2 )
r = 1 322,00 / 1 361,23
Az összefüggés a következő lesz:

Korreláció = 0,971177099
Relevancia és felhasználás
A statisztikákban főként a vizsgált változók közötti kapcsolat erősségének elemzésére használják, és ezenkívül azt is méri, hogy van-e lineáris összefüggés az adott adatsorok között, és mennyire lehet összefüggésben. A korrelációban használt egyik általános mérőszám a Pearson-korrelációs együttható.
Ha egy változó megváltozik az értékében, és ezzel a másik változóval együtt változik az érték, akkor ennek a kapcsolatnak a megértése kritikus, mivel az előbbi változó értékével megjósolhatjuk az utóbbi változó értékének változását. A korrelációnak sokféle felhasználása van manapság ebben a modern korban, mint például a pénzügyi iparban, a tudományos kutatásban és hol nem. De fontos tudni, hogy az összefüggésnek három fő kapcsolattípusa van. Az első egy pozitív kapcsolat, amely azt állítja, hogy ha változik egy változó értéke, akkor a kapcsolódó változó változása ugyanabban az irányban történik. Hasonlóképpen, ha negatív kapcsolat van, akkor a kapcsolódó változó az ellenkező irányba fog viselkedni. Továbbá, ha nincs összefüggés, akkor r nulla értéket jelent.A koncepció jobb megértéséhez lásd az alábbi képeket.









