Képlet a Sharpe arány kiszámításához
Sharpe arány = (R p - R f ) / σ pA Sharpe arány képletet a befektetők a kockázatmentes hozam feletti hozam, a portfólió volatilitásának egységére eső kiszámításához használják, és a képlet szerint levonják a várható portfólió hozamából a kockázat nélküli hozamot, és az eredményt elosztjuk a portfólió szórásával.

Hol,
- R p = A portfólió hozama
- R f = kockázatmentes arány
- σp = A portfólió többlethozamának szórása.
Hogyan lehet kiszámítani a Sharpe arányt?
- A Sharpe arány kiszámításakor a portfólió hozamának és a kockázatmentes kamatláb különbségét elosztjuk a portfolió többlethozamának szórásával. Ezen keresztül a kockázatmentes hozam alapján értékelhetjük a befektetési teljesítményt.
- A magasabb Sharpe mutató mindig jobb, mint egy alacsonyabb, mert a magasabb arány azt jelzi, hogy a portfólió jobb befektetési döntést hoz.
- A Sharpe arány azt is megmagyarázza, hogy a portfólió többlethozama jó befektetési döntés vagy túl sok kockázat következménye. Minél magasabb a kockázat magasabb hozam, alacsonyabb kockázat csökkenti a hozamot.
- Ha egy portfólió egyikének magasabb a hozama, mint versenytársainak, akkor ez jó befektetés, mivel a hozam magas és a kockázat ugyanaz. A megtérülés maximalizálásáról és a volatilitás csökkentéséről szól. Ha bármely befektetés megtérülési rátával rendelkezik, akkor a 15% és a volatilitás nulla. Ekkor a Sharpe arány végtelen lesz. A volatilitás növekedésével a kockázat jelentősen megnő, mivel a megtérülési ráta is növekszik.
Lássuk a Sharpe arány osztályozási küszöbét.
- <1 - Nem jó
- 1-1,99 - Ok
- 2-2,99 - Nagyon jó
- > 3 - kivételes
A nulla kockázatú portfólió csak a kincstárjegyet kedveli, mivel a befektetés kockázatmentes, nincs volatilitás és a kockázatmentes kamatlábat meghaladó bevétel. Így a Sharpe arány nulla portfólióval rendelkezik.
- Az 1., 2., 3. mutatónak magas a kockázati aránya. Ha a mutató 3 felett vagy egyenlő, akkor az nagyszerű Sharpe-mérésnek és jó befektetésnek számít.
- Míg ez egy nagyobb vagy egyenlő 1 és 2 közötti, 2-nél kisebb metrika, akkor csak oknak tekintjük, és ha egy metrika nagyobb vagy egyenlő 2 és háromnál kisebb, akkor azt tartják, hogy ez nagyon jó .
- Ha egy mutató kisebb, mint egy, akkor azt nem tekintik jónak.
Példák
1. példa
Tegyük fel, hogy két befektetési alapot kell összehasonlítani a különböző kockázati szinttel rendelkező különböző portfóliókkal. Most nézzük meg a Sharpe arányt, hogy melyikük teljesít jobban.
A Mid Cap részvényalap befektetése és részletei a következők: -
- Portfólió hozama = 35%
- Kockázatmentes ráta = 15%
- Szórás = 15
Tehát a Sharpe Ratio kiszámítása a következő lesz:
- Sharpe Ratio egyenlet = (35-10) / 15
- Sharpe arány = 1,33
A Bluechip Alap befektetése és részletei a következők: -
- Portfólió hozama = 30%
- Kockázatmentes ráta = 10%
- Szórás = 5
Tehát a Sharpe Ratio kiszámítása a következő lesz:
- Sharpe arány = (30–10) / 5
- Sharpe arány = 4
Ezért a fenti befektetési alap Sharpe-mutatói a következők:
- Bluechip Alap = 4
- Mid Cap alap = 1,33
A blue-chip befektetési alap felülmúlta a Mid cap befektetési alapot, de ez nem jelenti azt, hogy a Mid cap befektetési alap a kockázati szintjéhez képest jól teljesített volna. A Sharpe a következőket mondja el nekünk: -
- A blue-chip befektetési alap a befektetéssel járó kockázathoz képest jobban teljesített, mint a Mid cap befektetési alap.
- Ha a Mid cap befektetési alap ugyanolyan jól teljesít, mint a Blue-chip befektetési alap a kockázat szempontjából, akkor magasabb hozamot érne el.
- A blue-chip befektetési alap jövedelme magasabb az idén, de mivel a kockázat magas. Ezért a jövőben nagy volatilitása lesz.
2. példa
Itt egy befektető 5,00 000 dolláros befektetett portfóliót tart, várható megtérülési rátája 12%, volatilitása 10%. A hatékony portfólió 17% feletti megtérülést és 12% -os volatilitást vár. A kockázatmentes kamat 4%. A Sharpe arány kiszámítása az alábbiak szerint történhet: -
- Sharpe arány = (0,12 - 0,04) / 0,10
- Sharpe arány = 0,80
Sharpe Ratio kalkulátor
Használhatja a következő Sharpe Ratio kalkulátort.
| Portfólió visszaküldése | |
| Kockázatmentes arány | |
| A portfólió többlethozamának szórása | |
| Éles arány képlet = | |
| Éles arány képlet = |
|
|
Előnyök
A Sharpe arány előnyei a következők:
- Az arány az egységnyi volatilitás vagy a teljes kockázat egy kockázatmentes arányát meghaladó átlagos hozam
- A Sharpe arány segít a befektetések összehasonlításában.
- A Sharpe arány segít a kockázat-hozam összehasonlításban.
A Sharpe-arány használata során felmerül néhány olyan probléma, hogy azt a feltételezést alkalmazzák, hogy a befektetési hozam általában megoszlik, és ennek eredményeként a Sharpe-arány releváns értelmezése félrevezető.
Sharpe arányszámítás az Excelben
Az alábbiakban megadott sablon tartalmazza a közepes tőkeértékű befektetési alapok és a Bluechip befektetési alapok adatait a Sharpe arány kiszámításához.
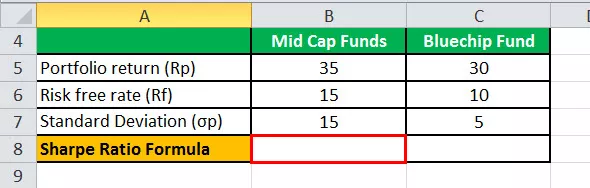
Az alábbiakban megadott excel sablonban a Sharpe arány egyenletének kiszámítását használtuk a Sharpe arány kiszámításához.

Tehát a Sharpe Ratio kiszámítása

Ajánlott cikkek:
Ez a Sharpe Ratio Formula útmutatója. Itt megvitatjuk, hogy a befektetők hogyan használják ezt a képletet a befektetés megtérülésének megértéséhez a kockázattal szemben, gyakorlati példákkal és Számológéppel együtt. A következő cikkekből többet tudhat meg a portfóliókezelésről -
- Számolja ki a kockázatmentes arányt
- Számítsa ki a Treynor arányt
- Részvények és a befektetési alapok közötti különbségek
- Hogyan tehet karriert a portfóliókezelésben?