Mi az a tartomány képlete?
A tartomány képlete arra a képletre vonatkozik, amelyet a tartomány maximális és minimális értéke közötti különbség kiszámításához használnak, és a képlet szerint a minimális értéket levonják a maximális értékből a tartomány meghatározásához.
Tartomány = a maximális érték - a minimális érték
Az adott adatkészletből, amely statisztikusoknak és a matematikusnak jobban megismeri az adatsort, mennyire változatos. A statisztikák szórásának kiszámítása a legegyszerűbb módszer.
Magyarázat
Ez meglehetősen egyszerű és könnyen használható, mivel a képlet megadja annak maximális értékét, az adott minta minimális értékével csökkentve. Ezért a maximális és a minimális érték közötti szórás a Tartomány, és bár ezt egyszerűen lehet használni és megérteni, megfelelő értelmezésre van szükség.
Például, ha van egy körvonalazó az adatokban, a tartományt ugyanez befolyásolja, és az eredmény félrevezetéshez vezet. Vegyünk egy gyakorlati példát a megadott 2, 4, 7, 7, 100 adatokra, akkor a tartomány 100 - 2 lenne, ami 98, de mivel láthatjuk, hogy az adattartomány 10 alatt van, de figyelembe véve és értelmezve, hogy az adatok 98-on belül vannak félrevezetéshez vezet. Ezért a Tartomány értelmezését kellő figyelemmel kell elvégezni.
Példák
1. példa
Fontolja meg a következő 2,2,4,4, 4, 6,7,7,8, 8, 8, 9, 9, 9, 9, 9 adatkészletet. A minta tartományát ki kell számolnia.
Megoldás:
- Maximális érték = 9
- Minimális érték = 2
Tartomány = 9 - 2
Tartomány = 7
2. példa
Stark úr, tudós, aki 10 évig dolgozik a Dream moon nevű céggel. Arora úr, témavezetője kísérletet folytat az emberi egészségre, és néhány férfi magasságú mintadatot gyűjtött össze, amelyek 162, 158, 189, 144, 151, 150, 151, 178, 155, 160. Most már megzavarodott, és tudni akarja, mennyi adat változik. Stark urat, aki tapasztalt statisztikus, felügyelője, Arora kereste meg, hogy kiküszöbölje a képlet variációjával kapcsolatos zavartságát. Arora úrnak választ kell adnia felügyelőjének; ki kell számolnia, hogy mennyire változnak az adatok?
Megoldás:
Tartomány = maximális érték - minimális érték
- Maximális érték = 189
- Minimális érték = 144
Tartomány = 189 - 144
Tartomány = 45
Az összegyűjtött adatok vagy a minta eltérése 45.
3. példa
Buffet úr, a világ minden tájáról ismert és megbecsült befektető, most fontolgatja az amerikai piaci részvényeket, és néhányukat elemzi, ahol befektetni akar. A listán az Egyesült Államok jelentős blue-chip cégei találhatók. Az alábbiakban bemutatjuk az adott rövid listán szereplő részvényeket vagy értékpapírokat, valamint a legutóbbi tőzsdei árat, amelyet USA dollárban jelölnek, ahol fontolgatja a befektetést.
Számítania kell a Tartományt, és elő kell állítania a listában szereplő változatot.
Megoldás:
Az alábbiakban adunk adatokat a tartomány kiszámításához.
A fenti információk felhasználásával a Max érték kiszámítása az excelben a következő lesz,

Maximális érték = 204,66
A minimális érték kiszámítása az excelben az alábbiak szerint,
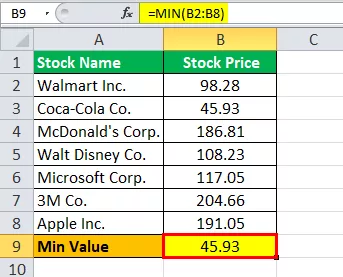
Minimum = 45,93
Ezért a tartomány kiszámítása a következő,

Tartomány = 204,66 - 45,93
A tartomány a következő lesz:
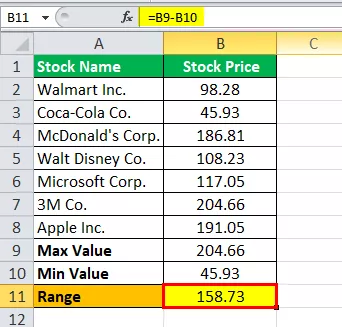
Tartomány = 158,73
A Range Formula felhasználása
A tartomány a maga módján nagyon könnyen és nagyon egyszerűen megérti, hogy az adott adathalmazban vagy adott mintában található számok hogyan oszlanak meg, mert mint korábban említettük, viszonylag könnyű elvégezni a számítást, mivel van csak egy nagyon alapvető számtani műveletre van szükség, amely éppen levonja a minimumot a maximális értékből, de a tartományban kevés további alkalmazás van egy adott adathalmazra vagy egy adott statisztikai mintára. A tartomány hasznos egy másik terjedési mérték becslésében is, amelyet varianciának vagy szórásnak hívunk.
A tartomány, amint azt korábban említettük, csak az alapvető részletekről tud tájékoztatni, vagyis arról, hogy egy adott minta vagy adott adatsor elterjedése hol található. Azáltal, hogy megadja a különbséget, vagy mondjuk a szórást az adott minta vagy adott adatkészlet legmagasabb és legalacsonyabb értéke között, egy információt vagy durva képet ad a jelentős szélsőséges megfigyelésekről, hogy ezek mennyire elterjedtek, de megint nem ad utalás vagy bármilyen információ, mint a többi adatpontra, hogy hol fekszenek, ami a tartományi egyenlet használatának fő gyengesége.
A tartomány, amint azt fentebb tárgyaltuk, hasznos az eloszlás ábrázolásához egy adott mintán vagy egy adott adatkészleten belül, és ezenkívül felhasználható az ugyanazon adott minta vagy ugyanazon adott adatkészletek közötti eredő különbség összehasonlítására is.








