Legkisebb négyzetek regressziós módszerének meghatározása
A legkisebb négyzetes regressziós módszer a regresszióanalízis egy olyan formája, amely a lineáris vonallal együtt létrehozza a kapcsolatot a függő és független változó között. Ezt a sort a „legjobban illeszkedő vonalnak” nevezik.
A regresszióanalízis olyan statisztikai módszer, amelynek segítségével megbecsülhetjük vagy megjósolhatjuk az egyik változó ismeretlen értékeit egy másik változó ismert értékeiből. A változó érdeklődésének előrejelzésére használt változót független vagy magyarázó változónak, az előrejelezni kívánt változót függő vagy magyarázott változónak nevezzük.
Tekintsünk két változót, az x & y-t. Ezeket egy grafikon ábrázolja, amelynek értéke x az y tengelyen lévő y x tengely értékein. Ezeket az értékeket a pontok képviselik az alábbi grafikonon. A pontokon egyenes vonal húzódik - a legjobban illeszkedő vonalnak nevezzük.

A legkisebb négyzetek regressziójának célja annak biztosítása, hogy a megadott értékhalmazon keresztül meghúzott vonal létrehozza a legszorosabb kapcsolatot az értékek között.
Legkisebb négyzetek regressziós képlete
A legkisebb négyzetek módszerrel a regressziós vonal kiszámítása a következő képlet segítségével történik:
ŷ = a + bx
Hol,
- ŷ = függő változó
- x = független változó
- a = y-metszéspont
- b = a vonal meredeksége
A b vonal meredekségét a következő képlet segítségével számoljuk ki:

Vagy

Y-metszet, az 'a' számítása a következő képlettel történik -

A Legjobb illesztés sora a legkisebb négyzet regresszióban
A legjobban illeszkedő egyenes az adatpontok szórásán keresztül húzott egyenes, amely a legjobban reprezentálja a köztük lévő kapcsolatot.
Vizsgáljuk meg a következő grafikont, ahol egy adatsort ábrázolunk az x és az y tengely mentén. Ezeket az adatpontokat a kék pontok ábrázolják. Három vonal húzódik ezeken a pontokon - egy zöld, egy piros és egy kék vonal. A zöld vonal egyetlen ponton, a piros vonal pedig három adatponton halad át. A kék vonal azonban négy adatponton halad át, és a maradék pontok és a kék vonal közötti távolság minimális a másik két vonalhoz képest.

A fenti grafikonon a kék vonal a legjobban illeszkedő vonalat jelöli, mivel az áll az összes értékhez legközelebb, és a vonalon kívüli pontok és a vonal közötti távolság minimális (azaz a maradványok és a legjobban illeszkedő vonal közötti távolság - a maradványok négyzetösszegeként is emlegetik). A másik két vonalban, a narancsban és a zöldben, a maradványok és a vonalak közötti távolság nagyobb, mint a kék vonal.
A legkisebb négyzetek módszer biztosítja a legszorosabb kapcsolatot a függő és független változók között azáltal, hogy minimalizálja a maradványok közötti távolságot, és a legjobban illeszkedő vonal, vagyis a maradványok négyzetének összege ebben a megközelítésben minimális. Ezért a „legkisebb négyzetek” kifejezés.
Példák a legkisebb négyzetek regressziós vonalára
Alkalmazzuk ezeket a képleteket az alábbi kérdésben -
1. példa
A technikusok vállalatban szerzett tapasztalatára (több évre) és teljesítményükre vonatkozó részleteket az alábbi táblázat tartalmazza. Ezen értékek felhasználásával becsülje meg a 20 év tapasztalattal rendelkező szakember teljesítményértékelését.
| Technikus tapasztalata (évek alatt) | teljesítmény-értékelés |
| 16. | 87 |
| 12. | 88 |
| 18. | 89 |
| 4 | 68 |
| 3 | 78 |
| 10. | 80 |
| 5. | 75 |
| 12. | 83. |
Megoldás -
Először a legkisebb négyzetek kiszámításához kiszámítjuk az Y-metszést (a) és a (b) egyenes meredekségét az alábbiak szerint:

A (b) vonal meredeksége

- b = 6727 - ((80 * 648) / 8) / 1018 - ((80) 2 /8)
- = 247/218
- = 1,13
Y-metszés (a)

- a = 648 - (1,13) (80) / 8
- = 69,7
A regressziós egyenes kiszámítása az alábbiak szerint történik:

A képletben x értéke 20 helyett 20,
- ŷ = a + bx
- ŷ = 69,7 + (1,13) (20)
- ŷ = 92,3
A 20 éves tapasztalattal rendelkező technikus teljesítményértékelése a becslések szerint 92,3.
2. példa
Legkisebb négyzetek regressziós egyenlete az Excel használatával
A legkisebb négyzetes regressziós egyenlet kiszámítható az excel segítségével a következő lépésekkel -
- Adattábla beszúrása az Excelbe.

- Helyezzen be egy szóródiagramot az adatpontok felhasználásával.

- Helyezzen be egy trendvonalat a szóródiagramba.

- A trendvonal opciók alatt válassza ki a lineáris trendvonalat, és válassza ki az egyenlet megjelenítését a diagramon.

- Az adott excel-adatsor legkisebb négyzetes regressziós egyenlete megjelenik a diagramon.
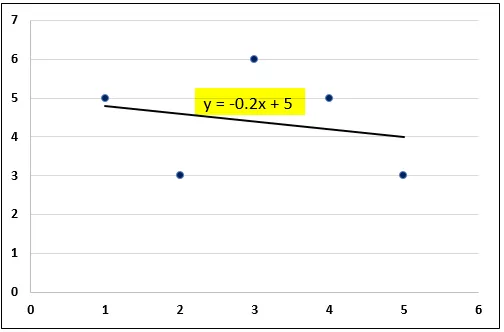
Így kiszámoljuk a legkisebb négyzetek regressziós egyenletét az adott excel adatkészlethez. Az egyenlet felhasználásával előrejelzések és trendelemzések készíthetők. Az Excel eszközei részletes regressziós számításokat is biztosítanak.
Előnyök
- A legkisebb négyzetes regresszióanalízis módszer a legalkalmasabb a predikciós modellekhez és a trendelemzéshez. A legjobban a közgazdaságtan, a pénzügyek és a tőzsdék területén alkalmazható, ahol bármely jövőbeli változó értékét megjósolják a meglévő változók és az ezek közötti kapcsolat segítségével.
- A legkisebb négyzetek módszer biztosítja a legszorosabb kapcsolatot a változók között. A maradványok négyzetösszege és a legjobban illeszkedő vonal közötti különbség ebben a módszerben minimális.
- A számítási mechanizmus egyszerű és könnyen alkalmazható.
Hátrányok
- A legkisebb négyzetek módszer a legszorosabb kapcsolat létrehozására támaszkodik egy adott változóhalmaz között. A számítási mechanizmus érzékeny az adatokra, és bármely kiugró érték (kivételes adat) esetén az eredmények nagyban befolyásolhatják.
- Ez a típusú számítás a legalkalmasabb a lineáris modellekhez. A nemlineáris egyenletek esetében teljesebb számítási mechanizmusokat alkalmaznak.
Következtetés
A legkisebb négyzetek módszer az egyik legnépszerűbb módszer az előrejelzési modellek és a trendelemzés során. Megfelelően kiszámítva a legjobb eredményt nyújtja.








